Numerically studying k-mers on k by L strips

This project is a part of the NIUS programme done under Prof. Deepak Dhar from ICTS Bangalore. The first part of the project (for about 2 months) involved reading and the extending the following paper’s work (), as well as reading about other topics in advanced statistical mechanics to get a feel for the tools I would be utilizing later on in the project.

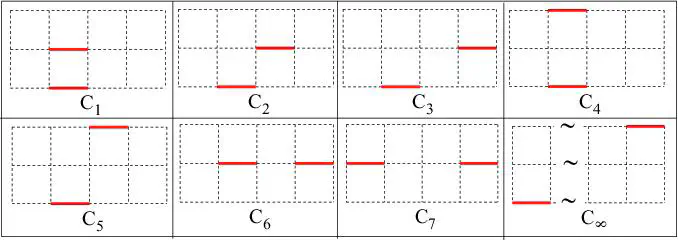
While Heilman and Lieb’s results for dimers on a 2D lattice model have been theoretically proven (and numerically verified in our draft, for a 2 by L strip), there has been no study done about trimers on a 3 by L strip, or in the more general setting, on a 2D lattice. In this project, I find two novel transfer matrix formulations for calculating the partition function encompassing all such configurations for a general L, and utilize some clever algebraic tricks to compress the size of the transfer matrices.

I obtain the surprising result that the zeroes of the partition function are bounded in the thermodynamic limit (checked both numerically, and by analyzing the characteristic polynomial of the transfer matrix). This has some interesting implications on the density (per unit length) of zeroes and its asymptotic form, as in the dimer scenario, since the zeroes are unbounded, the density function in the infinite activity limit is a constant. Finally, I developed and organised a new gradient-descent based algorithm to study the zeroes in a separate way, and obtain the density of zeroes numericallly from it.

Finally, the formalism developed in this project can be readily extended to higher values of k in the k by L strip, which can be then used to readily study the system of trimers on a 2D lattice.