Semidefinite Programming for understanding limitations of Lindblad Equations
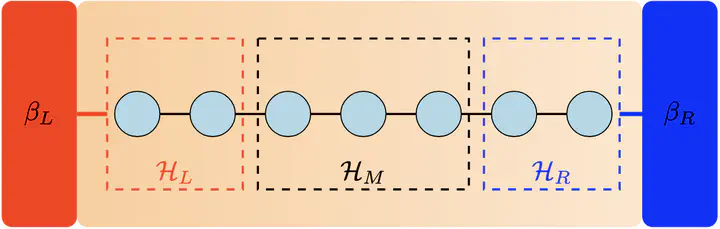 Photo taken from our a draft to be uploaded on arxiv soon
Photo taken from our a draft to be uploaded on arxiv soonThis project is a part of the LTVSP Fellowship done with Dr. Manas Kulkarni from ICTS Bangalore. The first part of this project involved investigating the fundamental limitations of Lindblad-form Quantum Master Equations (QMEs) in modeling open quantum systems. We tested whether a QME can simultaneously be physically consistent (i.e., completely positive and trace-preserving), satisfy local conservation laws, and accurately reproduce the correct non-equilibrium steady state (NESS). To do this, we formulated these desirable properties as a convex optimization problem, solvable using Semidefinite Programming (SDP). This method numerically searches for the “best possible” Lindbladian and returns two metrics, $\tau_{\text{opt}}^{\text{pop}}$ and $\tau_{\text{opt}}^{\text{pop, coh}}$, which are zero if a valid QME exists and non-zero if it is impossible. We applied this framework to XXZ and XX spin chains, specifically comparing systems with one ($N_L=N_R=1$) and two ($N_L=N_R=2$) qubits coupled to thermal baths at different temperatures.
For the single-qubit coupled setup, our numerics revealed that both $\tau_{\text{opt}}^{\text{pop}}$ and $\tau_{\text{opt}}^{\text{pop, coh}}$ were consistently far above our zero-tolerance, establishing a rigorous no-go result: no valid Markovian QME can capture the correct steady-state populations or coherences in this non-equilibrium regime. In contrast, for the two-qubit coupled setup, we found that $\tau_{\text{opt}}^{\text{pop}}$ dropped below the tolerance, indicating that finding a QME that correctly models populations is possible. However, $\tau_{\text{opt}}^{\text{coh}}$ remained high, proving it is still fundamentally impossible for the QME to also capture the correct steady-state coherences.
In the second part, I provided analytical backing for these no-go results. I formally derived a rigorous lower bound for the trace distance between the exact zeroth-order NESS and the steady state of any locally-conserving Lindbladian QME. I prove this bound is directly proportional to our numerically-optimized $\tau_{\text{opt}}$, analytically confirming that if $\tau_{\text{opt}}$ is non-zero (as our numerics showed), a finite, unavoidable error between the true steady state and any possible Lindblad model is guaranteed. The work is currently in preparation as a manuscript.